In this problem, we wish to build a wall out of bricks that are 2 by 1 in dimension. The wall, in this example, will always be two units tall and form a rectangular shape. We are given illustrations of the different arrangements for the first three walls and asked:
Given the length of a wall, determine how many patterns there may be for a wall of that length.
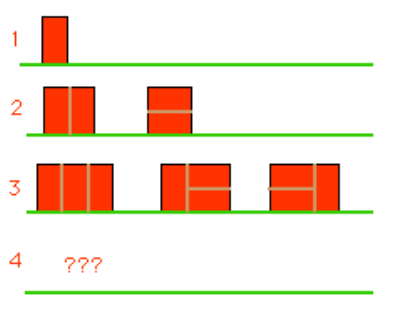
With our goal defined, we may begin by manually drawing out the next few walls. For a wall of length 4, there are 5 possible arrangements:
|||| ||= |=| =|| ==For a wall of length 5, there are 8 possible arrangements:
||||| |||= ||=| |=|| =||| |== =|= ==|Now, if you're at all acquainted with the Fibonacci sequence , this pattern of the number of wall configurations should look very familiar, right? Let's review the definition. Leonardo Fibonacci's numbers are defined as,
Let's code up a simple recursive implementation to find the value of the nth Fibonacci number:
Just to validate our suspicions, we'll print the first ten Fibonacci numbers and compare them with our number of wall arranges for a wall of length n.
From this, we see that the number of wall configurations, for a wall of length n, is equal to the value returned by fib(n + 1).
Implementation
Our input comes in the form of a sequence of positive integers, one per line, which represents the length of a wall. The largest possible input is 50. This problem also has a time limit of 3.000 seconds, and our recursive implementation will be doing a LOT of extra work calculating Fibonacci numbers up to 50 for every input query. Since the input specified by the problem statement does not specify a maximum number of test cases to process, it should hint at the possibility of combining subproblems and reusing solution values as you process consecutive test cases. Thus, this problem is a good candidate for Dynamic Programming , or DP.
Using Dynamic Programming to find Fibonacci numbers up to 50
Essentially, rather than computing the nth Fibonacci number recursively (i.e., top-down), we are going to use the base cases of fib(0) = 0, fib(1) = 1 to compute the remaining Fibonacci numbers in the range [2..50] using a bottom-up technique. All we need is an array that can hold 52 elements (i.e., 50 max wall length, plus 1 to accommodate 0-based indexing, plus 1 because the number of configurations for wall length n is fib(n + 1)), our base cases, and a for-loop. Also, we need to make sure we use a value type larger than int or even unsigned int. A value type of long long will be sufficient because it is guaranteed the target type will have a width of at least 64 bits (since C++11). . For reference, the 51st Fibonacci number has a value greater than 20 billion; far too large to store in 32 bits.
That's it! You may commonly see the DP technique in problem types involving optimization, counting, and min/maxing. As long as you are aware of the method (and practice it, of course!), you'll be able to recognize and quickly code up elegant solutions to otherwise challenging problems.